Design an Optimal Decision Tree based Algorithm to Improve Model Prediction Performance
Main Article Content
Abstract
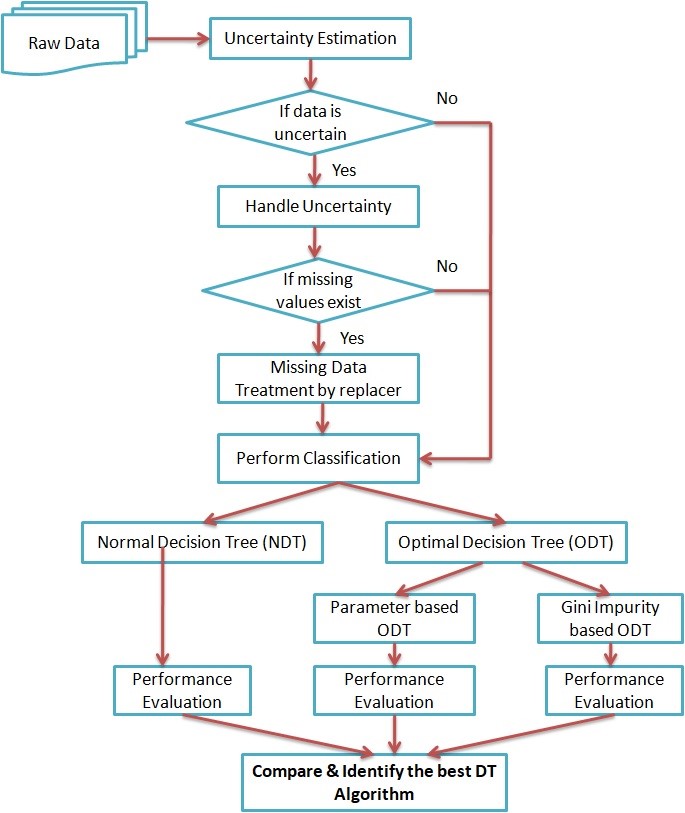
Performance of decision trees is assessed by prediction accuracy for unobserved occurrences. In order to generate optimised decision trees with high classification accuracy and smaller decision trees, this study will pre-process the data. In this study, some decision tree components are addressed and enhanced. The algorithms should produce precise and ideal decision trees in order to increase prediction performance. Additionally, it hopes to create a decision tree algorithm with a tiny global footprint and excellent forecast accuracy. The typical decision tree-based technique was created for classification purposes and is used with various kinds of uncertain information. Prior to preparing the dataset for classification, the uncertain dataset was first processed through missing data treatment and other uncertainty handling procedures to produce the balanced dataset. Three different real-time datasets, including the Titanic dataset, the PIMA Indian Diabetes dataset, and datasets relating to heart disease, have been used to test the proposed algorithm. The suggested algorithm's performance has been assessed in terms of the precision, recall, f-measure, and accuracy metrics. The outcomes of suggested decision tree and the standard decision tree have been contrasted. On all three datasets, it was found that the decision tree with Gini impurity optimization performed remarkably well.
Article Details
References
Meyer ,P. E. & Bontempi, G. On the use of variable complementarity for feature selection in cancer classification. Workshops on applications of evolutionary computation, 2006. Springer, 9102.
Mingers, J. 1989. An empirical comparison of pruning methods for decision tree induction. Machine learning, 4, 227-243.
Painsky, A. & Rosset, S. 2016. Cross-validated variable selection in tree-based methods improves predictive performance. IEEE transactions on pattern analysis and machine intelligence, 39, 2142-2153.
Pande, A., Li, L., Rajeswaran, J., Ehrlinger, J., Kogalur, U. B., Blackstone, E. H. & Ishwaran, H. 2017. Boosted multivariate trees for longitudinal data. Machine learning, 106, 277-305.
Panhalkar, A. R. & Doye, D. D. 2021. Optimization of decision trees using modified African buffalo algorithm. Journal of King Saud University-Computer and Information Sciences.
Peng, H., Long, F. & Ding, C. 2005. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Transactions on pattern analysis and machine intelligence, 27, 1226-1238.
Probst, P. & Boulesteix, A.-L. 2017. To tune or not to tune the number of trees in random forest. J. Mach. Learn. Res., 18, 6673-6690.
Rahman, M. G. & Islam, M. Z. 2013. Missing value imputation using decision trees and decision forests by splitting and merging records: Two novel techniques. Knowledge-Based Systems, 53, 51-65.
Rahman, M. G. & Islam, M. Z. 2016. Missing value imputation using a fuzzy clustering-based EM approach. Knowledge and Information Systems, 46, 389-422.
Rokach, L. 2016. Decision forest: Twenty years of research. Information Fusion, 27, 111-125.
Setiawan, N. A., Venkatachalam, P. A. & Hani, A. F. M. Missing attribute value prediction based on artificial neural network and rough set theory. 2008 international conference on bioMedical engineering and informatics, 2008. IEEE, 306-310.
Sinharay, S., Stern, H. S. & Russell, D. 2001. The use of multiple imputation for the analysis of missing data. Psychological methods, 6, 317.
Song, Q., NI, J. & Wang, G. 2011. A fast clustering-based feature subset selection algorithm for high-dimensional data. IEEE transactions on knowledge and data engineering, 25, 1-14.
SONG, Y.-Y. & YING, L. 2015. Decision tree methods: applications for classification and prediction. Shanghai archives of psychiatry, 27, 130.
Tibshirani, R. & Hastie, T. 2007. Margin Trees for High-dimensional Classification. Journal of Machine Learning Research, 8.
Tsang, S., Kao, B., Yip, K. Y., Ho, W.-S. & Lee, S. D. 2009. Decision trees for uncertain data. IEEE transactions on knowledge and data engineering, 23, 64-78.
Tutz, G. & Ramzan, S. 2015. Improved methods for the imputation of missing data by nearest neighbor methods. Computational Statistics & Data Analysis, 90, 84-99.
Wang, S., Aggarwal, C. & Liu, H. 2018. Random-forest-inspired neural networks. ACM Transactions on Intelligent Systems and Technology (TIST), 9, 1-25.
Wang, S., Jiang, L. & Li, C. 2015. Adapting naive Bayes tree for text classification. Knowledge and Information Systems, 44, 77-89.
Wang, T., Qin, Z., Jin, Z. & Zhang, S. 2010. Handling over-fitting in test cost-sensitive decision tree learning by feature selection, smoothing and pruning. Journal of Systems and Software, 83, 1137-1147.
Wang, Y. & Zhang, N. 2014. Uncertainty analysis of knowledge reductions in rough sets. The Scientific World Journal, 2014.
Windeatt, T. & Ardeshir, G. An empirical comparison of pruning methods for ensemble classifiers. International Symposium on Intelligent Data Analysis, 2001. Springer, 208-217.
Xia, Y., Liu, C., Li, Y. & Liu, N. 2017. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Systems with Applications, 78, 225-241.
Yager, R. R., Zadeh, L. A., Kosko, B. & Grossberg, S. 1994. Fuzzy sets, neural networks, and soft computing.
Yan, J., Zhang, Z., Xie, L. & Zhu, Z. 2019. A unified framework for decision tree on continuous attributes. IEEE Access, 7, 11924-11933.
Ye, Y., Wu, Q., Huang, J. Z., Ng, M. K. & Li, X. 2013. Stratified sampling for feature subspace selection in random forests for high dimensional data. Pattern Recognition, 46, 769-787.
Zadeh, L. A. 1996. Soft computing and fuzzy logic. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi a Zadeh. World Scientific.
Zhang, Z., Zhao, Z. & Yeonm, D.-S. 2020. Decision Tree Algorithm-Based Model and Computer Simulation for Evaluating the Effectiveness of Physical Education in Universities. Complexity, 2020.
Zhao, L., Lee, S. & Jeong, S.-P. 2021. Decision Tree Application to Classification Problems with Boosting Algorithm. Electronics, 10, 1903.
Zharmagambetov, A., Gabidolla, M. & Carreira-Perpinan, M. A. Improved multiclass AdaBoost for image classification: The role of tree optimization. 2021 IEEE International Conference on Image Processing (ICIP), 2021. IEEE, 424-428.