Pseudo Random Binary Sequences Obtained Using Novel Chaos Based Key Stream Generator and their Auto-correlation Properties

Article Sidebar

PDF
Published: May 17, 2023
DOI: https://doi.org/10.17762/ijritcc.v11i5.6588
Keywords:
Pseudo Random Numbers (PRN’s), Chaos Based Cryptography, Auto Correlation test, Stream Ciphers, Data Security

Main Article Content

Pushpalatha G S
Research Scholar, Department of Electronics & Communication Engineering, Dr. Ambedkar Institute of Technology, Visvesvaraya Technological University Belagavi, India
Ramesh S
Professor, Department of Electronics & Communication Engineering, Dr. Ambedkar Institute of Technology, Visvesvaraya Technological University Belagavi, India

Abstract

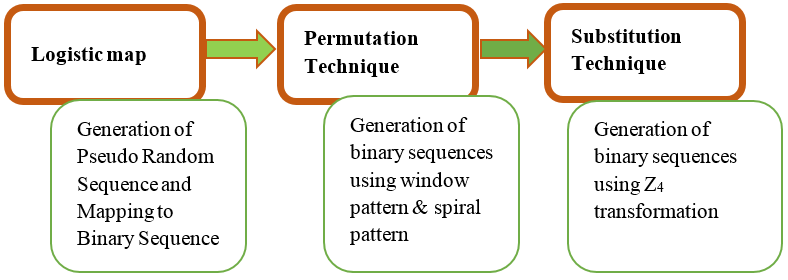
In this paper, psuedo random binary sequences are generated from the “Chaos Based Key Stream Generator- using novel Permutation technique with two dimensional patterns and substitution technique with Z4 mapping” and investigation of auto correlation property for the generated seuwnces is presented. Initially a chaotic function, considering Logistic map is used to generate a Pseudo Random Numbers (PRNs). Then these numbers are converted into binary sequences using binary mapping. These sequences are further modified by novel permutation techniques defined using 2-Dimensional patterns, and substitution technique defined over Z4 transformation in order to improve their statistical properties. The resulting sequences are investigated for auto correlation properties using Normalized Hamming Auto Correlation function. The purpose of this work is to assessing the quality of sequences of uniformly distributed pseudorandom numbers from the proposed generator. It is found that, generated sequences exhibit good auto-correlation property which is suitable for key sequence or secret key for cryptographic applications.

Article Details

How to Cite
G S, P. ., & S, R. . (2023). Pseudo Random Binary Sequences Obtained Using Novel Chaos Based Key Stream Generator and their Auto-correlation Properties. International Journal on Recent and Innovation Trends in Computing and Communication, 11(5), 141–147. https://doi.org/10.17762/ijritcc.v11i5.6588
Issue
Vol. 11 No. 5 (2023): May (2023) Issue
Section
Articles

References

Alfred J Menezes, Paul C. Van Oorschot and Scott A. Vanstone, “Handbook of Applied Cryptography”, CRC Press, New York, 1997.

William Stallings, “Cryptography and Network Security”, Principles and Practice, 5th Edition, Pearson Education Inc, 2006.

Francois Panneton and Pierre L’Ecuyer, “Random Number Generators Based on Linear Recurrences in”, Monte Carlo and Quasi-Monte Carlo Methods, Niederreiter H., Editor, Springer-Verlag, 2004, pp.367-378, 2002.

Francois Panneton and Pierre L’Ecuyer, “On the Xorshift Random Number Generators'', ACM Transactions on Modeling and Computer Simulation, 15, 4, pp 346-361, 2005.

Francois Panneton, Pierre L'Ecuyer, Makoto Matsumoto , “Improved Long-period Generators Based on Linear Recurrences Modulo 2”, ACM Trans. Math. Software. 32(1): pp.1-16. 2006.

Bernstein G. M. and Lieberman M. A., “Secure Random Number Generation Using Chaotic Circuits”, IEEE Trans. Circuits Syst., Vol. 37, No. 9, pp. 1157-1164, 1990.

Claude Shannon, “Communication Theory of Secrecy Systems”, Bell System Technical Journal, 28 (4), pp 656–715, 1949.

R. Matthews, “On the derivation of a chaotic encryption algorithm”, Cryptologia, XIII (1), pp 29–42, 1989.

Madhekar Suneel, “Cryptographic Pseudo-random Sequences from the Chaotic Henon Map”, Sadhana, Indian Academy of Sciences, Vol. 34, Part 5 , pp. 689–701, 2009.

Vinod yt Patidar and Sud K. K., “A Pseudo Random Bit Generator Based on Chaotic Logistic Map and its Statistical Testing”, Informatica 33, pp. 441–452, 2009.

Kitsos p., D. Gligoroski et al, “On the Hardware Implementation of the Mickey-128 Stream Cipher”, Cryptology ePrint Archive, Report, Presented in the eSTREAM publications List, pp 301, 2005.

Kitsos P., Kaiser U., “A high-speed Hardware Implementation of the Hermes 8-128 Stream Cipher”, European Conference on Circuit theory and Design- Seville, pp. 364-367, 2008.

Li Shujun, Mou Xuanqin, Cai Yuanlong, “Pseudo-Random Bit Generator Based on Couple Chaotic Systems and its Applications in Stream-Cipher”, Indocrypt,LNCS, 2001.

P. Kitsos and A. N. Skodras, “On the Hardware Implementation of the MUGI Pseudorandom Number Generator”, In proceedings of the Fifth International Symposium on Communications Systems, Networks and Digital Signal Processing, Patras, Greece, 2006.

Kitsos P., G. Kostopoulos, Sklavos N., and Koufopavlou O. , "Hardware Implementation of the RC4 Stream Cipher”, 46th IEEE Midwest Symposium on Circuits & Systems, Cairo, Egypt, pp. 27-30,2003.

Matt J. B. Robshaw, “Stream Ciphers Technical Report-TR-701”, Version 2.0 (RSA Laboratories), 1995.

Goresky M. and Klapper A, “Algebraic Shift Register Sequences”, Cambridge university press, pp. 230-249, 2012.

Soloman Wolf Golomb, “Shift Register Sequences”, San Francisco:Holden Day, Reprint Aegan Park Press, Laguna Hills, California,1967.

Dieter Gollmann and William G. Chambers, “Clock-Controlled Shift Registers: a Review”, IEEE Journal on Selected Areas in Communications, 7(4), pp. 525–533, 1989.

Ekdahl P and Johansson T, SNOW-A New Version of the Stream Cipher SNOW, Selected Areas in Cryptography, (Springer-Verlag), LNCS 2595, pp. 47-61, 2003.

Soloman Wolf Golomb and Guang Gong, “Signal Design for Good Correlation for Wireless Communication, Cryptography and Radar”, Cambridge University Press, 2005.

Ramesh, S; Murali, R; Haribhat, KN, “Generation of Sequence of Random Numbers defined over Z4 and their correlation properties”, International Conference on Communication Technology. IEEE, pp 1-4, 2006.